Experimental Horror Game

---

TeamMates

• Elena I. G. - No portfolio available
• Morgan James - Portfolio
• Kyle Banford - No portfolio available

Documentation

In my team for this project we had two designers and two programmers. I was the first programmer and Morgan james was the other. Since there were so many members working on the same project we had to split up the work. My contribution to the project was mainly the 3D dungeon crawling game. Morgan worked on the other two games and together we worked on the rest of the games code.

In the creation of this maze mini-game there are two main systems. The first is the map generation script and the second is pathfinding so that the enemy can find the player.

Pathfinding

The pathfinding algorithm is a basic implementation of the A* pathfinding algorithm that is so popular in game development. With almost the same efficiency of Greedy Best First Search (GBFS) and the reliability of Dijkstra’s algorithm it is clearly the best choice for pathfinding through this maze. Especially since the maze is built on a grid structure.

Below is an image depicting the visual representation of the pathfinding in the mini-game.

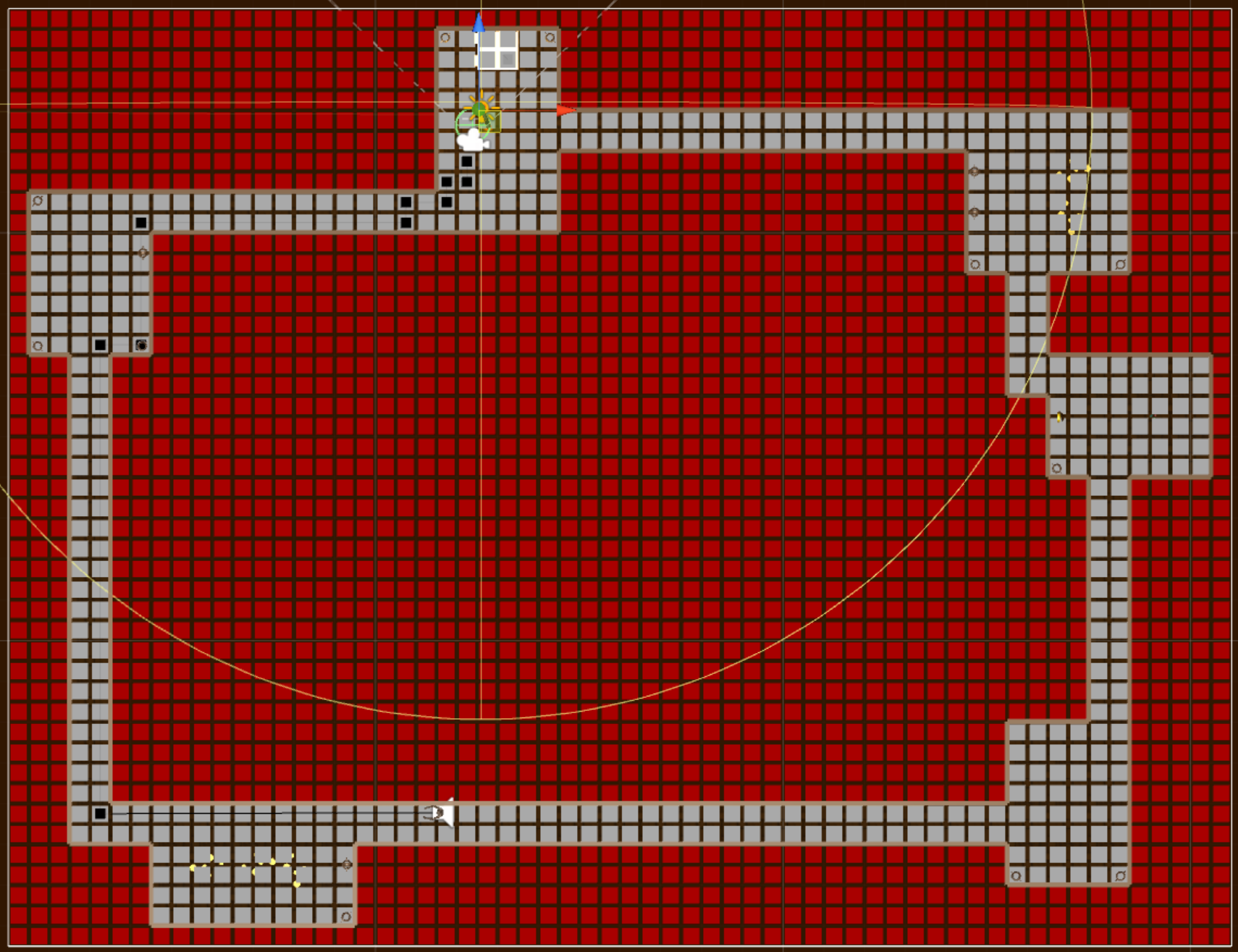
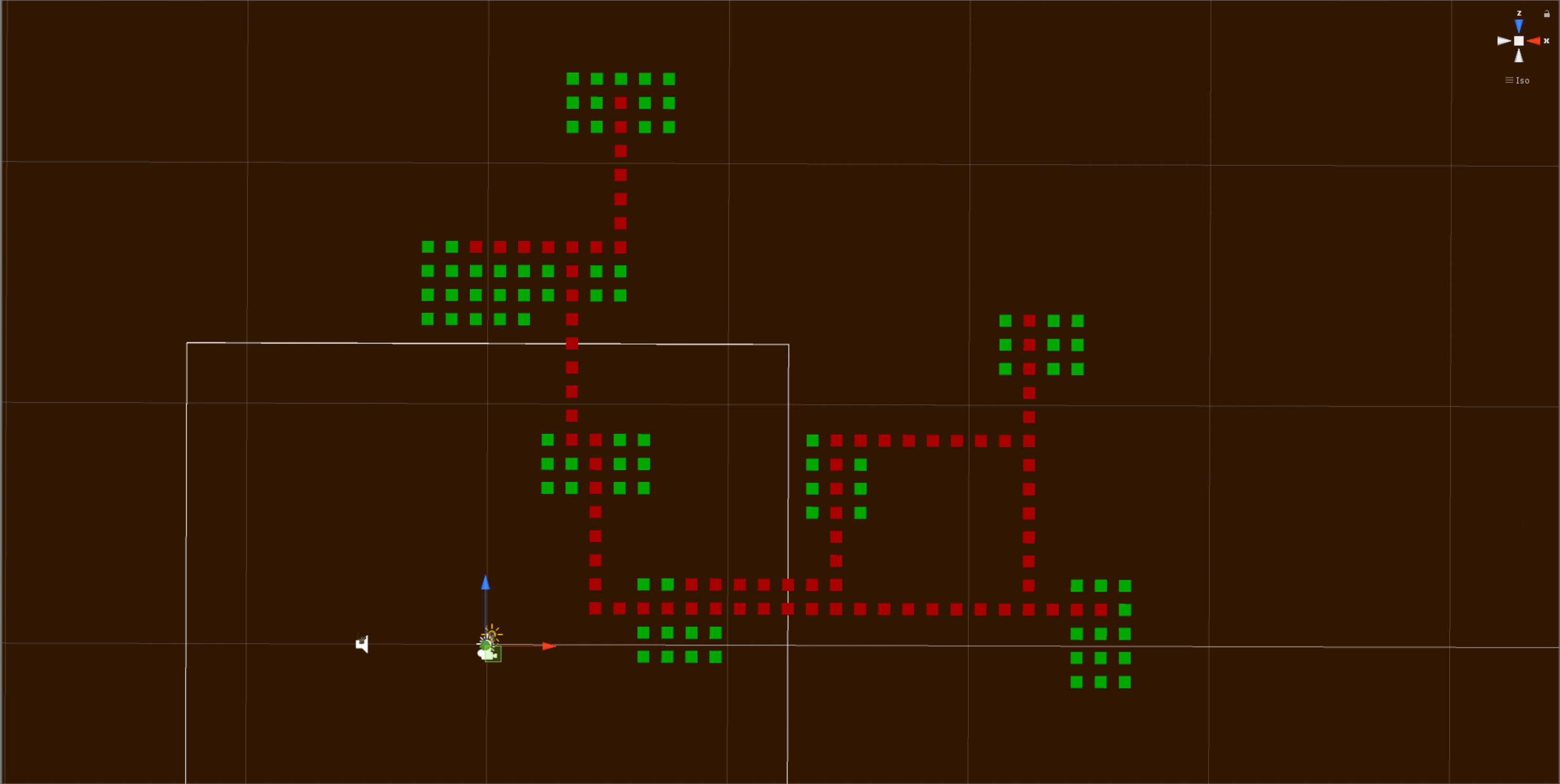
In this image you can see a few things going on, let me explain. The squares represent a grid on which the A* algorithm can operate. The grey squares are walkable and the red squares cannot be traversed. You can also see a series of smaller black squares with black lines connecting them. This is the completed path from a source to a destination on this grid.

This A* pathfinding algorithm operates on a grid (it doesn’t always have to), it first picks one position as a starting point and one position as a destination. From this it can extrapolate a path of nodes (usually just positions on the grid) that lead you from the source to the destination. I won’t be explaining the full algorithm here as there are plenty of better resources for that.

Map Generation

Before I start explaining this section I would like to state that my map generation is heavily inspired, and is very similar to, another dungeon generation algorithm from the game ‘Tiny Keep’. The creator of Tiny Keep, Phi Dinh, explains this algorithm much better than me in a post on reddit.

In between screenshots I will be needing to restart the map generation so the example maps that are built are always going to look different, however, you should still be able to see what is happening.

To start we have to create a grid in which to put all of our map items in. This should have a random width and height. Then we need to generate some rooms, these should also have a random width and height however, they should not be square. The positions of the rooms should be random within the grid however, it’s best if they are weighted so that the majority spawn near to the middle whilst fewer spawn close to the edges. This distribution should be a bell curve.

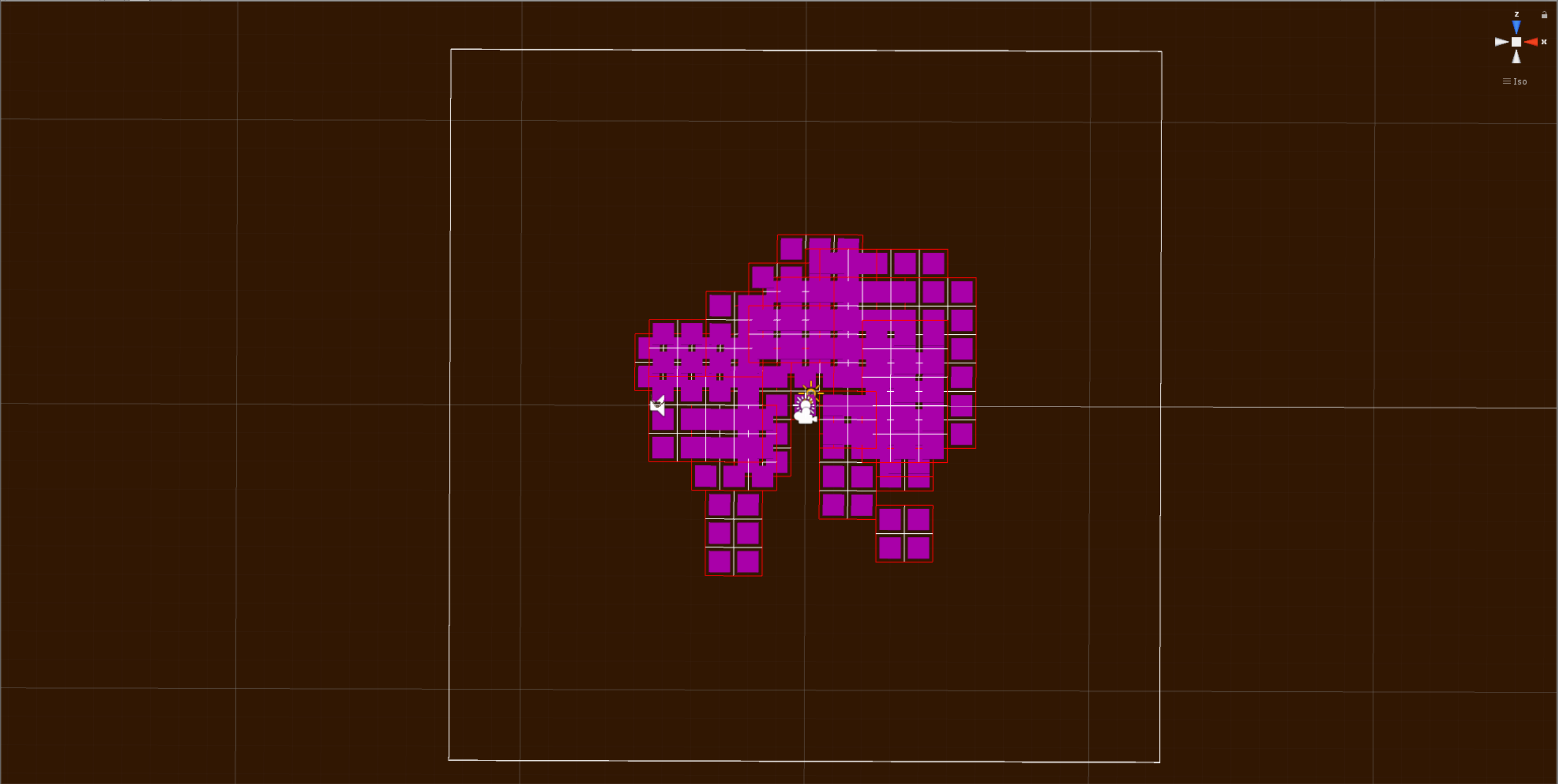
After we have some rooms we need to separate them.

We then need to choose some rooms to create the maze with, generally speaking rooms that have an area that is higher than the average area of all the rooms are good. These rooms are now referred to as active rooms and are grey as opposed to pink.

We will then relocate all of the rooms so that the average position of all of them is the exact center of the world, the xyz coordinates for this are (0, 0, 0).

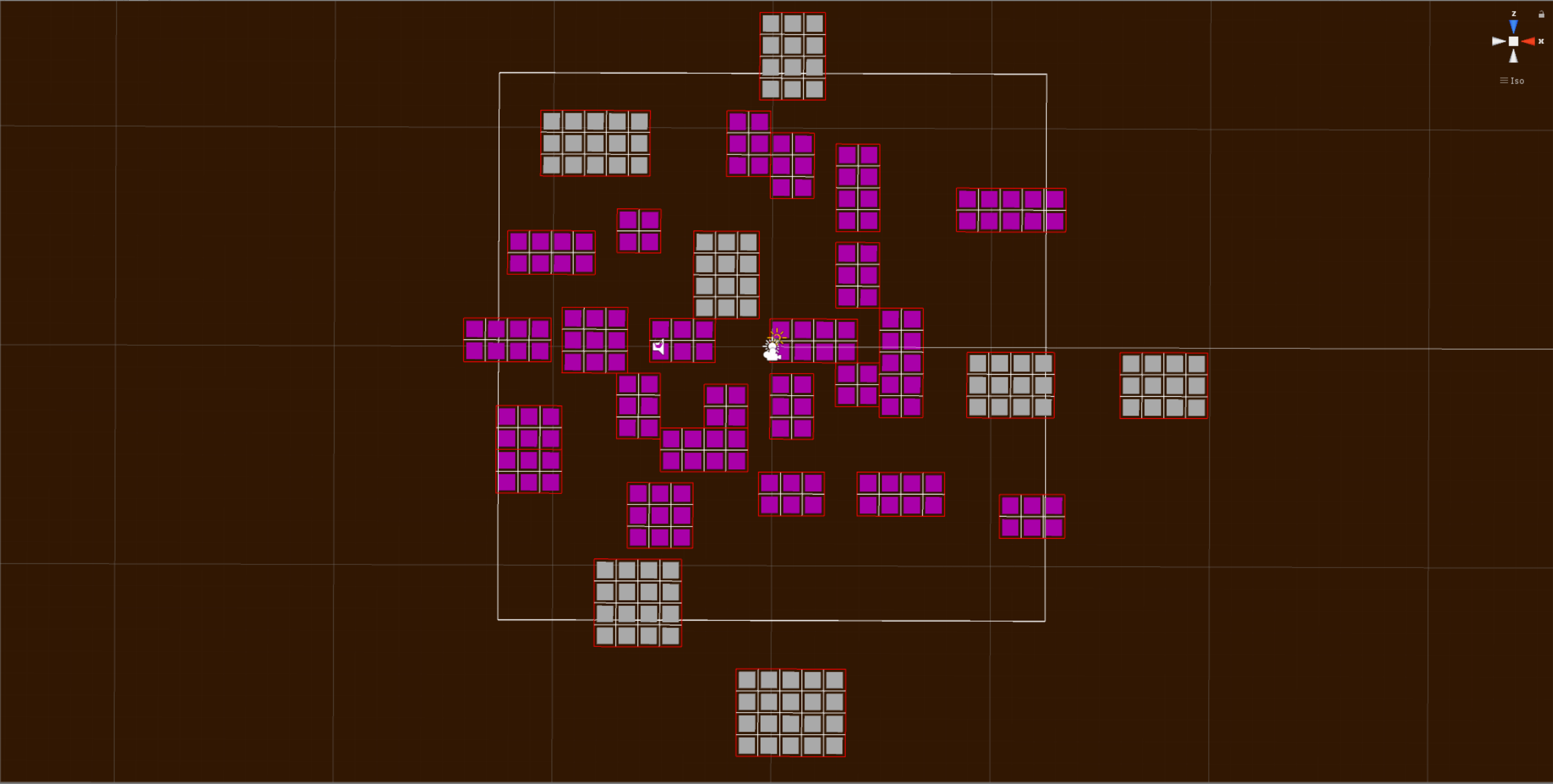
The rooms are then aligned to the maze ‘grid’ meaning that their positions will always be multiples of 1.

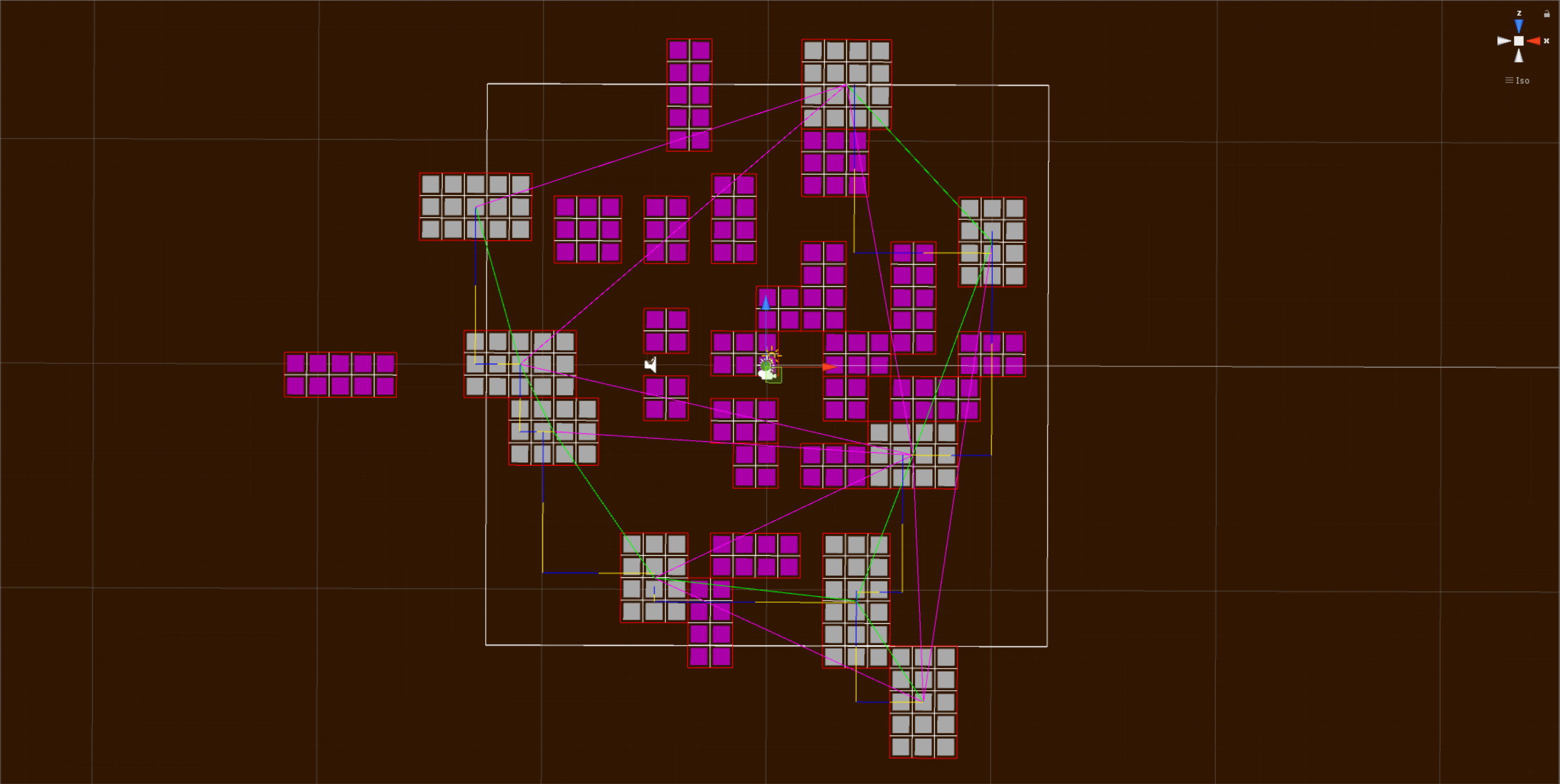
The next section is a little complicated so I used an open-source library to do the difficult stuff for me. We need to create a Delaunay triangulation of the currently active (grey) rooms. Put simply this is just creating a series of lines that connect all of the rooms without any overlapping. The lines in pink make up the Delaunay triangulation.

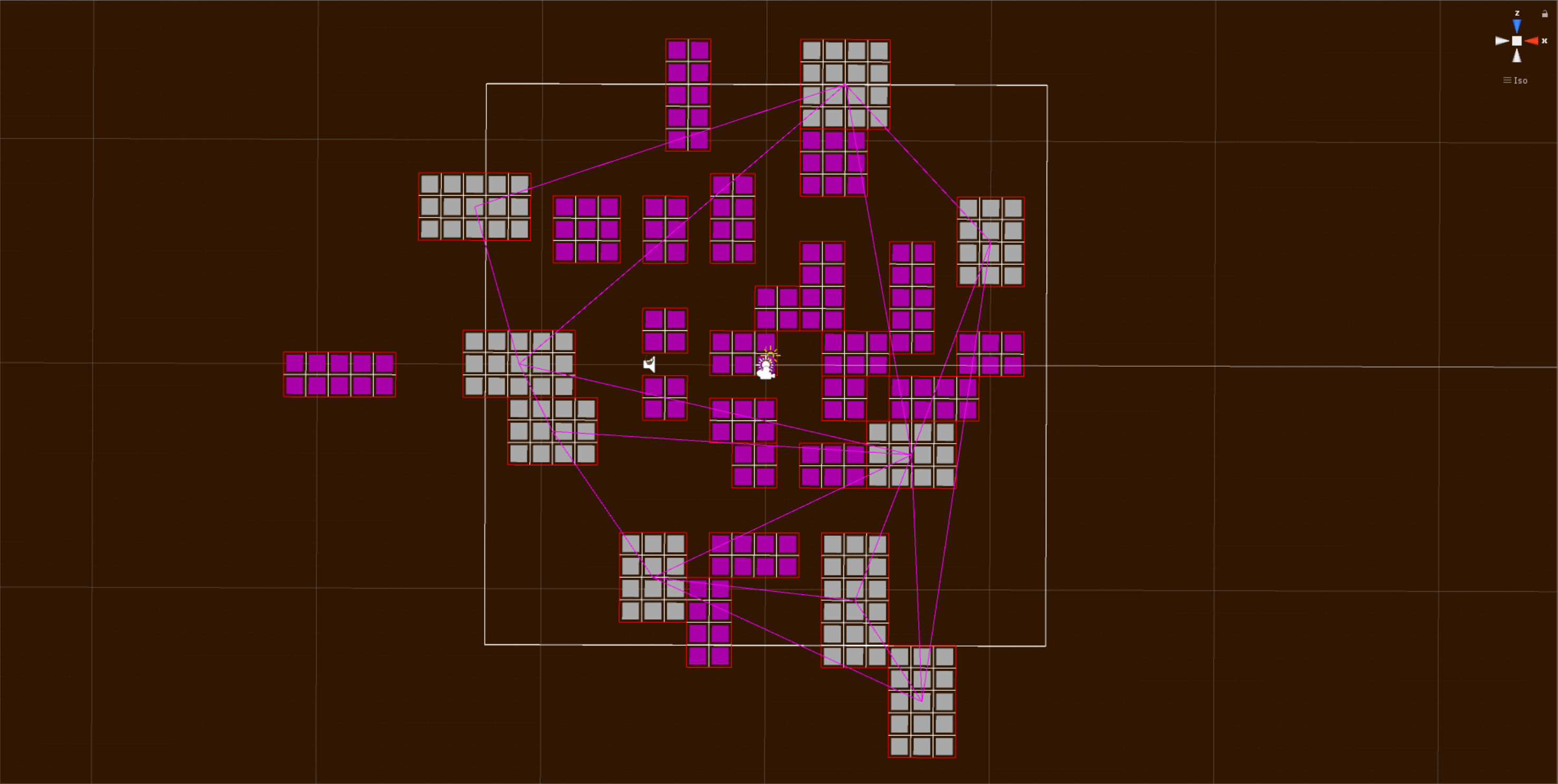
From the Delaunay triangulation we need to create a minimum spanning tree. This means that we need to find the minimum amount of lines it would take to connect all the rooms. The lines that create the Delaunay triangulation come from the center of the rooms. The lines in green make up the minimum spanning tree.

Next we need to create corridors from the minimum spanning tree. To do this we need to think back to trigonometry, but more specifically right angle triangles. If we assume that the lines in the minimum spanning tree (green lines) are the hypotenuse of a right angle triangle then we can use formulas, created by smarter people than me, to find the length of the both the opposite and adjacent sides of the triangle. The blue and yellow lines make up the map corridors.

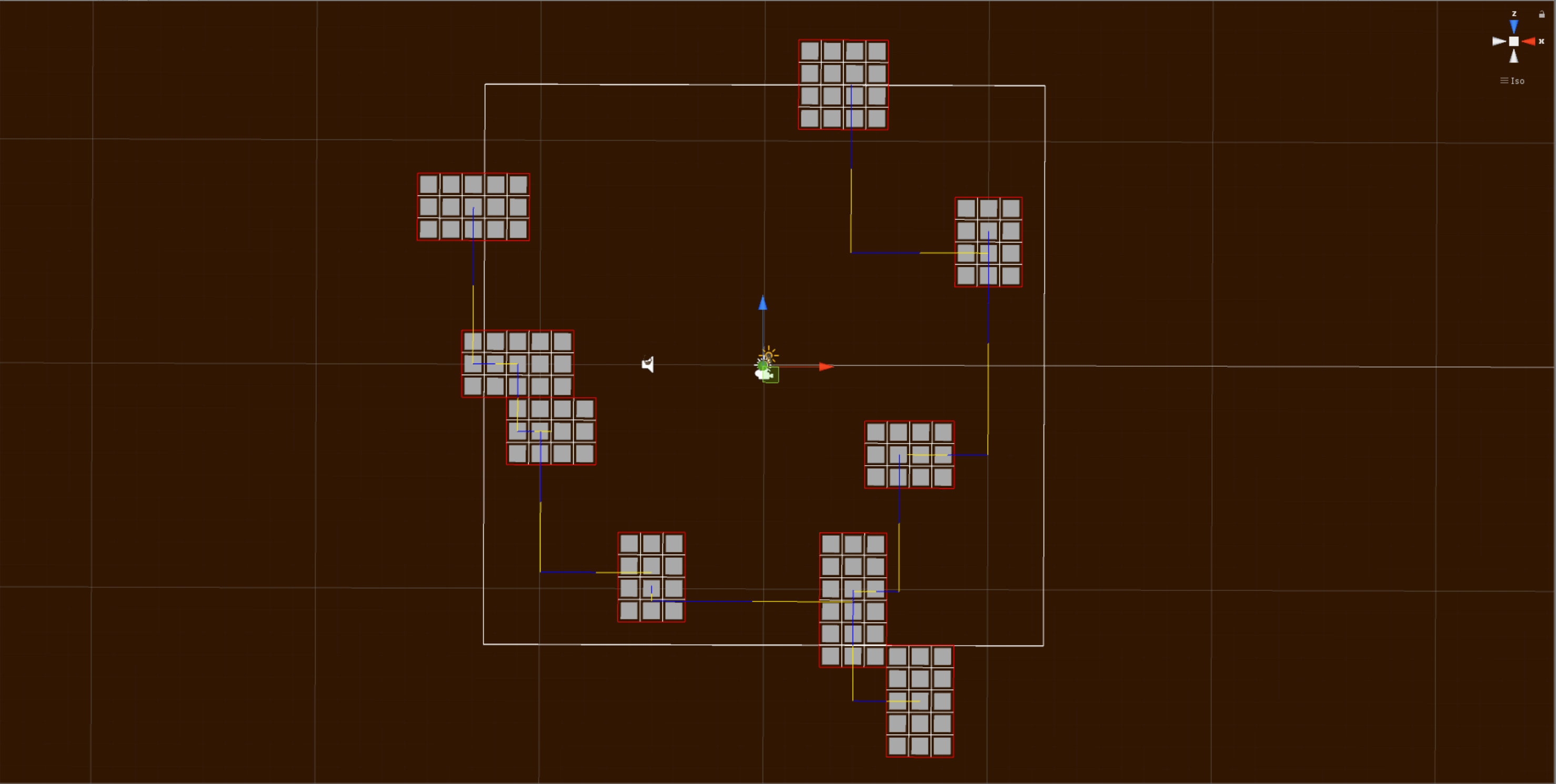
Here is an image similar to the one above, however, this just shows the active cells and the corridors.

At this point the algorithm should add in inactive rooms that intersect with corridor lines however, my implementation of this, for whatever reason, has been very unstable. All my attempts to fix it has led to crashing and so I did the best I could with the time I was given and it sort of works. Since this is such a minor feature of the map generation my team and I didn’t deem it a top priority to fix it and so we left this problem to the end of the project and didn’t have time to change it.

The next part of the generation is a little theoretical. We need to take the rooms and corridors we have created so far and apply them to a tile map. A tile map is a two dimensional grid made up of square tiles of equal size (represented by numbers such as 0, 1, 2, etc.). This tile map will be used later when we come to spawning actual game objects in the world.

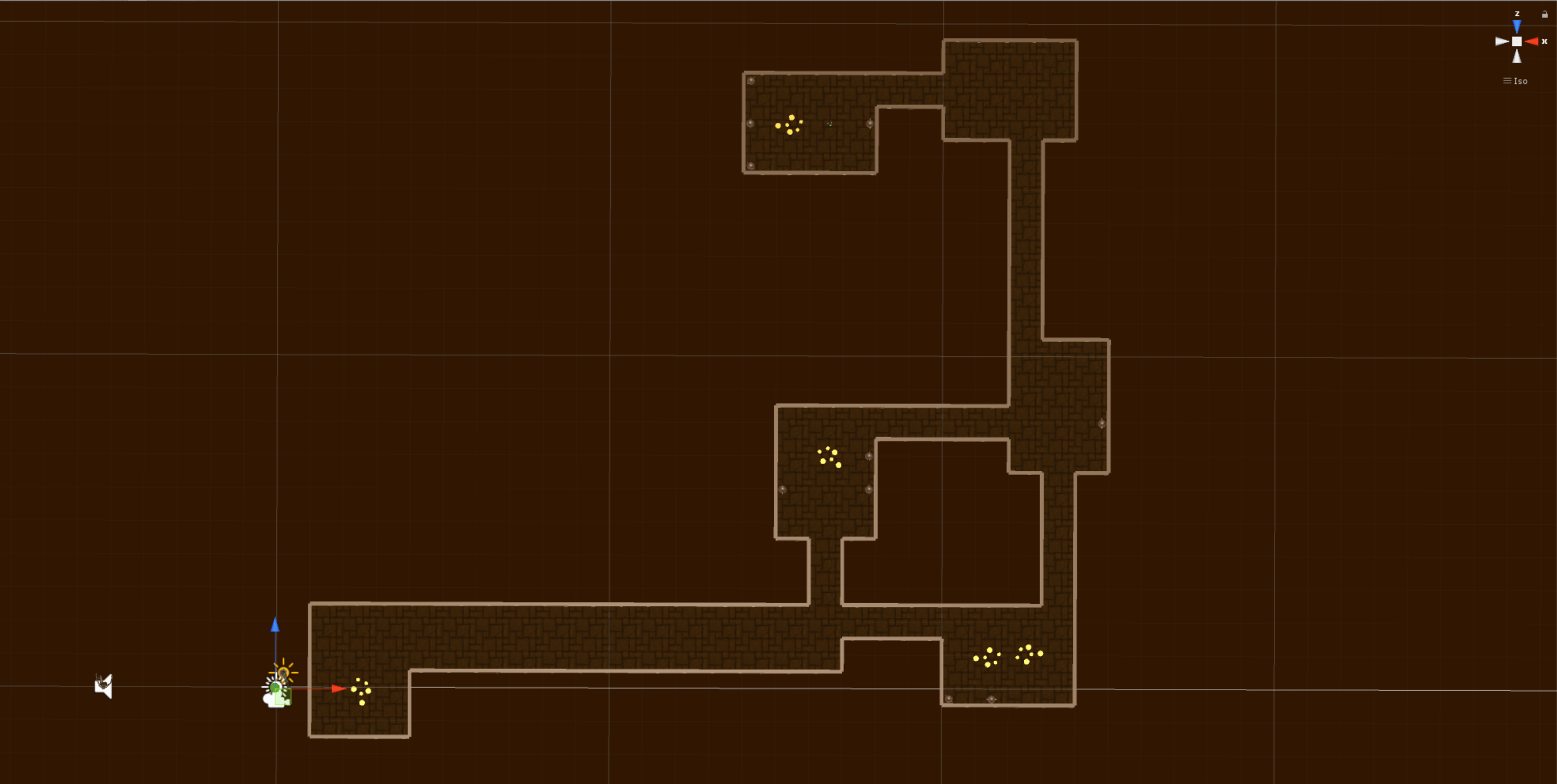
We can then use the tile map to spawn in all the objects we need. This image of the map is from above and I have removed the roof. The spawning of objects is done in three stages. The first stage is to spawn the floors, after this we can do some checks and spawn walls on the empty edges of the floors, finally we can place scenic objects randomly in the maze along with the player, enemy, and exit.

We are now entering the final stages of the map generation. We need to fit the pathfinding grid around the map as shown below.

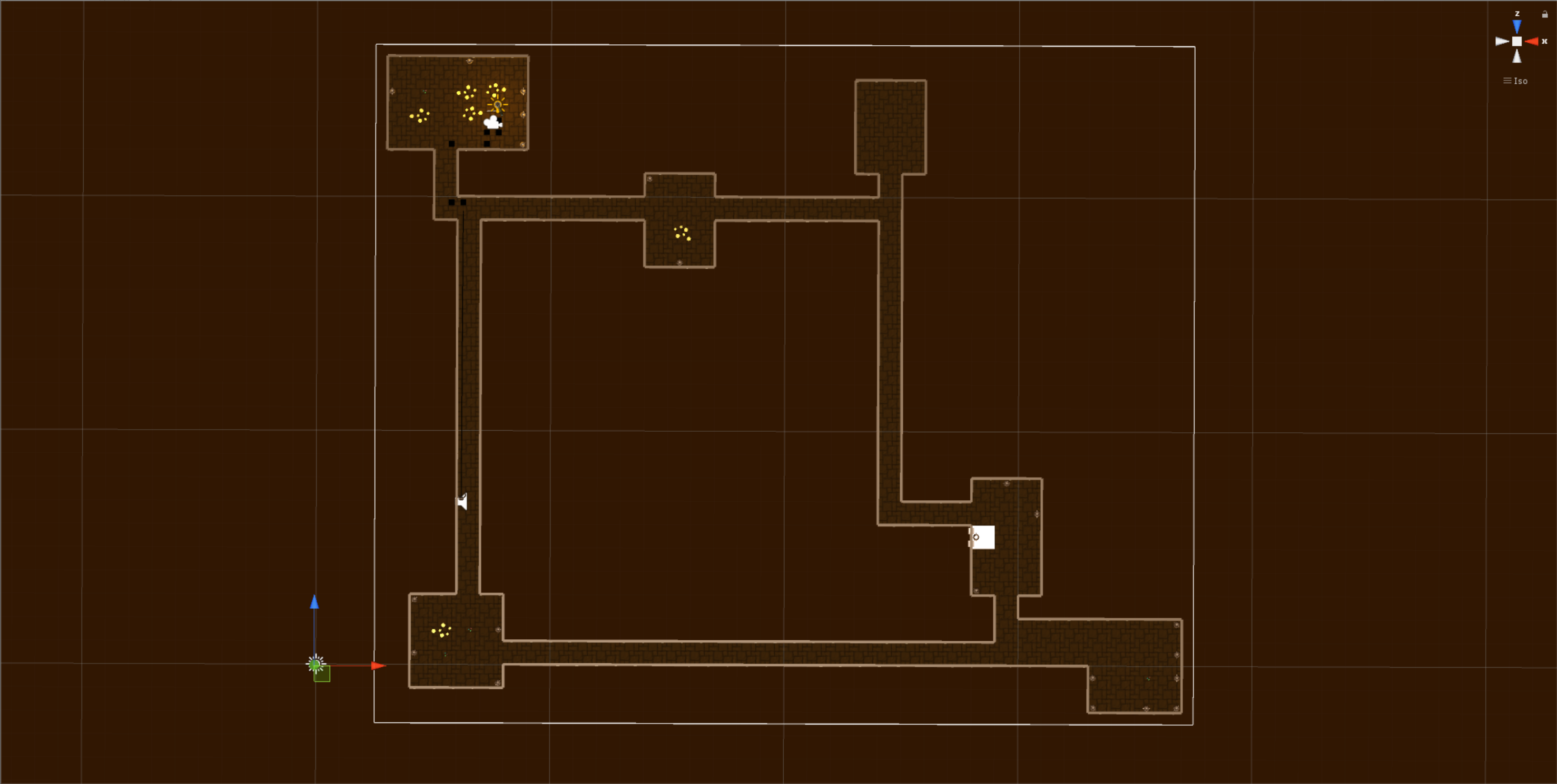
The final step in the map generation involves two things. We need to use the pathfinding grid to try to find a path from the player to the exit, and from the enemy to the player. This map generation is pretty reliable but it does have its glitches every now and then so we need to make sure that these things can reach each other. If both of these pathfinding checks come back ok then we can let the player take control and have fun, however, if the checks come back false then we need to clear everything we have just done and start again.

Map Generation Efficiency

The code for the map generator is written in C#. Initially when creating the generator I thought that the best way to handle all the code would be to run it in a coroutine (IEnumerator). However, although this did allow a moving screen to keep the player entertained during the load it slowed the loading time down to around 13 seconds. In an attempt to try to keep the animated loading screen but also speed the generation up I tried passing the generation code to a thread. I found out the hard way that Unity doesn’t have a very good implementation (as of version 5.6.1f1). Passing the load to a thread cause the generation time to drop from the previous 13 seconds to an astonishing 0.5 seconds. What an improvement! However, it came at a slight cost: 50% of the time Unity would crash. This left me in a slight dilemma, do I have a super fast loading but very unstable game, or a boredom inducing one? In the end I went with a compromise between the two. I still wanted the fast speed of a thread, but the stability of the IEnumerator. So I scrapped the threading idea and instead had the code run on the main thread. This would effectively halt all other operations but if the map generation stayed within the average generation time (0.5 seconds) it was acceptable.